원리금균등상환 원금균등상환 차이(저당상수표 엑셀 다운)

원리금균등상환 원금균등상환

대출은 내 집 마련이나 개인 사업, 재테크 등 다양한 목적을 위해 사용되지만, 상환 방식에 대한 이해가 필수적입니다.

 

원리금균등상환은 매달 같은 금액을 갚으며, 초기에는 이자 비중이 높고 점차 원금 비중이 커지는 방식입니다.

 

반면, 원금균등상환은 매달 동일한 원금을 갚고, 이에 따라 이자가 점점 줄어드는 방식입니다.

 

이번 포스팅에서는 이 두 상환 방식의 차이를 알아보고, 각자의 재정 상황에 맞는 최적의 선택을 할 수 있도록 도와드리겠습니다.

원리금균등상환 원금균등상환

두 방식의 이해

 

원금균등상환과 원리금균등상환 방식에 대해 알아보겠습니다.

 

이름만 보면 조금 딱딱하게 느껴질 수 있지만, 사실 대출을 받을 때 누구나 마주하게 되는 중요한 개념입니다.

 

대출을 갚는 방법이 바로 이 두 가지 방식 중 하나로 진행되기 때문입니다.

 

예를 들어, 은행이나 금융기관에서 대출을 신청하면 직원이 "원금균등상환으로 하시겠습니까, 아니면 원리금균등상환으로 하시겠습니까?"라고 묻거나, 각 방식에 따라 상품을 제시할 것입니다.

 

이때 각 방식의 차이를 이해하고, 본인에게 맞는 상환 방법을 선택하는 것이 중요합니다.

 

두 방식의 차이점은 무엇일까요?

 

간단히 말해, 원금균등상환은 매달 동일한 금액의 원금을 갚아나가는 방식입니다.

 

이 방식은 시간이 지나면서 이자가 줄어들어, 전체적으로 지불해야 하는 이자가 적어집니다.

 

반면, 원리금균등상환은 매달 동일한 금액의 원금과 이자를 합친 금액을 갚는 방식으로, 초기에 이자 비중이 크고 점차 줄어드는 구조입니다.

 

어느 방식이 더 유리할까요?

 

결론부터 말씀드리면, 원리금균등상환이 원금균등상환보다 전체적으로 더 많은 이자를 내게 됩니다.

 

하지만 월 상환액이 일정하여 예산을 관리하기는 쉽습니다.

 

반면, 원금 균등 상환은 초반에 월 상환액이 크지만 시간이 갈수록 줄어들고, 전체적으로 지불하는 이자가 적습니다.

 

이 두 방식의 차이를 이해하면, 대출을 갚아나가는 동안 발생하는 비용을 좀 더 정확하게 예측할 수 있고, 재정 상황에 맞는 최적의 상환 방식을 선택하는 데 큰 도움이 될 것입니다.

 

원리금이란

원리금이라는 용어가 다소 낯설게 느껴지실 수 있습니다.

 

원리금은 대출을 받았을 때 갚아야 할 총 금액을 말하며, 여기에는 빌린 돈인 '원금'과 그에 따른 '이자'가 포함됩니다.

 

쉽게 말해, 원리금은 대출받은 금액에 이자를 더한 총 상환 금액을 의미합니다.

 

이자가 붙는 구조

이자 계산

 

이자 계산 방식을 1억 원 대출 예시로 설명드리겠습니다.

 

대출을 받으실 때 이자가 매년 부과되는 금액은 '잔금'입니다.

 

잔금은 대출받은 원금에서 이미 상환한 금액을 제외한, 아직 갚지 않은 금액을 의미합니다.

 

예를 들어, 1억 원을 처음에 대출받으셨다고 가정해보겠습니다.

 

이때 원금은 1억 원입니다. 1년 후에 2천만 원을 상환하셨다면, 남은 원금은 8천만 원이 됩니다.

 

이 8천만 원이 바로 잔금이며, 매년 이자가 이 잔금에 대해 부과됩니다.

 

첫 해에는 원금이 1억 원이므로, 만약 이자율이 10%라면 첫 해의 이자는 1천만 원이 됩니다.

 

2천만 원을 갚고 나서 잔금이 8천만 원으로 줄어들면, 두 번째 해의 이자는 이 8천만 원에 대해 부과되므로 800만 원이 됩니다.

 

다음 해에도 2천만 원을 상환하면 잔금이 6천만 원이 되고, 그 해의 이자는 6천만 원에 대한 10%, 즉 600만 원이 되는 식입니다.

 

이렇게 이자는 매년 갚고 남은 잔금에 부과되기 때문에, 원금을 상환할수록 이자도 점차 줄어듭니다.

 

원리금균등상환 원금균등상환 비교

원금 균등 상환과 원리금 균등 상환 방식의 차이를 1억 원 대출 예시로 설명드리겠습니다.

 

두 방식 모두 대출 상환 방식이지만, 상환하는 방식에 차이가 있다고 하였죠.

 

가정해보겠습니다: 1억 원을 대출받고, 5년 동안 갚아야 하며, 연이자율은 10%라고 해봅시다.

 

1. 원금균등상환 방식

 

원금균등상환 방식은 원금을 매년 동일하게 나누어 갚는 방식이죠.

 

1억 원을 5년 동안 균등하게 갚는다면, 매년 원금 2천만 원씩 갚게 됩니다.

 

이자는 매년 남은 원금(잔금)에 대해 부과되므로, 상환 초기에 이자 부담이 높지만 시간이 지날수록 줄어듭니다.

 

예를 들어, 첫 해에는 원금 2천만 원을 갚고, 잔금인 8천만 원에 대해 10%의 이자가 부과되어 800만 원의 이자를 추가로 지불하게 됩니다.

 

다음 해에는 원금 2천만 원을 더 갚아 잔금이 6천만 원이 되고, 이자 600만 원을 지불하는 식으로 이자가 점점 줄어듭니다.

 

2. 원리금균등상환 방식

 

원리금균등상환 방식은 매년 원금과 이자를 합친 금액을 동일하게 상환하는 방식입니다.

 

이 방식은 저당상수를 이용해 계산됩니다. 저당상수는 대출 기간과 이자율을 기준으로 정해지는 값인데, 예를 들어 5년 동안 10% 이자율로 대출을 받으면 저당 상수는 약 0.2638입니다.

 

이 저당 상수를 원금 1억 원에 곱하면 매년 갚아야 할 원리금이 나옵니다.

 

계산해보면, 1억 원 × 0.2638 = 약 2,638만 원이 됩니다.

 

즉, 원리금 균등 상환 방식에서는 매년 2,638만 원씩 고정된 금액을 갚아 나가면 됩니다.

 

3. 두 방식의 요약

 

원금균등상환: 매년 동일한 원금 2천만 원을 상환하고, 남은 잔금에 대한 이자를 추가로 지불합니다. 이자는 매년 줄어듭니다.

 

원리금균등상환: 저당 상수(0.2638)를 이용해 매년 2,638만 원씩 상환하며, 이 금액에는 원금과 이자가 모두 포함되어 있어 상환액이 매년 동일합니다.

 

저당상수표

 

No	이자율 (%)	5년	10년	15년	20년	25년	30년	35년
1	1	0.206	0.1056	0.0721	0.0554	0.0454	0.0387	0.034
2	2	0.2122	0.1113	0.0778	0.0612	0.0512	0.0446	0.04
3	3	0.2184	0.1172	0.0838	0.0672	0.0574	0.051	0.0465
4	4	0.2246	0.1233	0.0899	0.0736	0.064	0.0578	0.0536
5	5	0.231	0.1295	0.0963	0.0802	0.071	0.0651	0.0611
6	6	0.2374	0.1359	0.103	0.0872	0.0782	0.0726	0.069
7	7	0.2439	0.1424	0.1098	0.0944	0.0858	0.0806	0.0772
8	8	0.2505	0.149	0.1168	0.1019	0.0937	0.0888	0.0858
9	9	0.2571	0.1558	0.1241	0.1095	0.1018	0.0973	0.0946
10	10	0.2638	0.1627	0.1315	0.1175	0.1102	0.1061	0.1037

저당상수표 엑셀다운

위의 표가 필요한 분을 위해 엑셀로 만들어서 첨부하였습니다.

 

첨부된 엑셀은 이자율을 0.5% 단위로 더 쪼개서 35년까지 데이터를 넣어두었어요. 잘 활용하시기를 바랍니다.

 

저당상수표_35년까지 데이터.xlsx

0.01MB

 

 

원금균등상환 vs  원리금균등상환 비교 실전 예시

1억 원 대출을 기준으로 원금균등상환방식 그리고 원리금상환방식을 설명드리겠습니다.

 

대출 조건은 대출금 1억 원, 대출 기간 5년, 연이자율 10%입니다. 이 조건을 바탕으로 원금 균등 상환 방식에서 상환 구조를 살펴보겠습니다.

 

원금균등상환 실전

원금균등상환 그림

 

1억 원의 원금, 이자율 10%로 5년에 걸쳐 원금균등상환으로 갚는 것으로 실전 예시로 들어보겠습니다.

 

1. 첫 해

첫 해에는 1억 원에 대한 이자가 부과됩니다. 이자율이 10%이므로 이자는 1천만 원입니다.

 

따라서 첫 해에 갚아야 할 원리금 상환액은 원금 2천만 원과 이자 1천만 원을 합쳐 총 3천만 원이 됩니다.

 

원금 2천만 원을 갚고 나면 잔금은 8천만 원으로 줄어듭니다.

 

2. 두 번째 해

두 번째 해에는 잔금 8천만 원에 대해 10%의 이자가 부과되어, 이자는 800만 원이 됩니다.

 

원리금 상환액은 원금 2천만 원과 이자 800만 원을 더한 2,800만 원입니다. 이때 잔금은 6천만 원으로 줄어듭니다.

 

3. 세 번째 해

세 번째 해에는 잔금 6천만 원에 대한 이자가 부과되어, 이자는 600만 원입니다.

 

원리금 상환액은 원금 2천만 원과 이자 600만 원을 더한 2,600만 원입니다. 이후 잔금은 4천만 원이 됩니다.

 

4. 네 번째 해

네 번째 해에는 잔금 4천만 원에 대한 이자가 붙어, 이자는 400만 원이 됩니다.

 

원리금 상환액은 2,400만 원(2천만 원 + 400만 원)이며, 잔금은 2천만 원으로 줄어듭니다.

 

5. 다섯 번째 해

마지막 다섯 번째 해에는 잔금 2천만 원에 대해 이자가 200만 원 부과됩니다.

 

원리금 상환액은 2,200만 원(2천만 원 + 200만 원)이 되고, 이로써 대출 원금과 이자가 모두 상환됩니다.

 

요약

이와 같이 원금 균등 상환 방식에서는 매년 2천만 원씩의 원금을 갚아나가며, 이자는 매년 남은 잔금에 대해 부과되어 점차 줄어듭니다.

 

따라서 5년 동안의 총 상환 금액은 원금 1억 원과 총이자 3천만 원(1천만 원 + 800만 원 + 600만 원 + 400만 원 + 200만 원)을 합쳐 1억 3천만 원이 됩니다.

 

위의 과정을 표로 만들어 보았습니다. 원리금 상환액(원금 + 이자)을 다 합치면 1억 3천만 원이 나옵니다.

No	년도	상환 원금(만원)	잔금(만원)	연이자(만원)	원리금 상환액(만원)
1	1	2,000	10,000	1,000	3,000
2	2	2,000	8,000	800	2,800
3	3	2,000	6,000	600	2,600
4	4	2,000	4,000	400	2,400
5	5	2,000	2,000	200	2,200

 

원리금균등상환 실전

원리금균등상환 그림

 

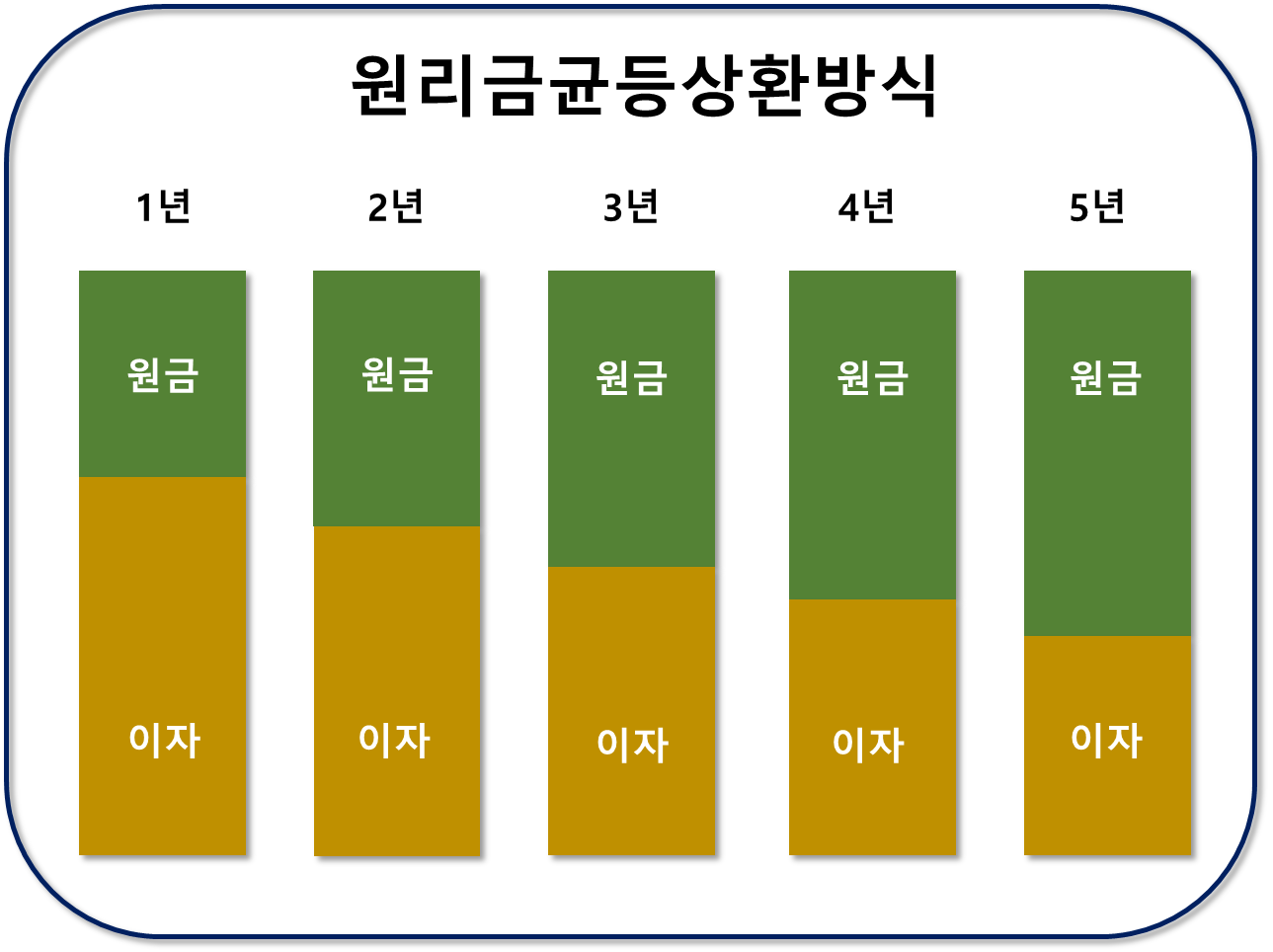
1억 원 대출 시, 5년 만기와 연이자율 10%의 저당 상수는 약 0.2638입니다.

 

따라서 1억 원에 저당 상수를 곱하면 매년 상환할 원리금은 약 2,638만 원이 됩니다.

 

이 금액은 5년 동안 매년 동일하게 상환하게 됩니다.

 

1. 첫 해

이자: 첫 해에는 원금 1억 원에 대해 이자율 10%가 적용되어 이자가 1,000만 원 발생합니다.

 

원금 상환액: 원리금 2,638만 원에서 이자 1,000만 원을 뺀 나머지 1,638만 원이 원금 상환액이 됩니다.

 

잔금: 1억 원에서 1,638만 원을 상환하여 잔금은 8,362만 원이 됩니다.

 

2. 두 번째 해

이자: 잔금 8,362만 원에 대해 10% 이자가 적용되어 836만 원이 부과됩니다.

 

원금 상환액: 원리금 2,638만 원에서 이자 836만 원을 빼면 1,802만 원이 원금 상환액이 됩니다.

 

잔금: 8,362만 원에서 1,802만 원을 상환하여 잔금은 6,560만 원이 됩니다.

 

3. 세 번째 해

이자: 잔금 6,560만 원에 대해 10% 이자가 적용되어 656만 원이 부과됩니다.

 

원금 상환액: 원리금 2,638만 원에서 이자 656만 원을 빼면 1,982만 원이 원금 상환액이 됩니다.

 

잔금: 6,560만 원에서 1,982만 원을 상환하여 잔금은 4,578만 원이 됩니다.

 

4. 네 번째 해

이자: 잔금 4,578만 원에 대해 10% 이자가 적용되어 458만 원이 부과됩니다.

 

원금 상환액: 원리금 2,638만 원에서 이자 458만 원을 빼면 2,180만 원이 원금 상환액이 됩니다.

 

잔금: 4,578만 원에서 2,180만 원을 상환하여 잔금은 2,398만 원이 됩니다.

 

5. 다섯 번째 해

이자: 잔금 2,398만 원에 대해 10% 이자가 적용되어 240만 원이 부과됩니다.

 

원금 상환액: 원리금 2,638만 원에서 이자 240만 원을 빼면 2,398만 원이 원금 상환액이 됩니다.

 

잔금: 잔금은 모두 상환되어 0원이 됩니다.

 

요약

5년 동안 원금 1억 원을 모두 상환하고, 총 이자는 약 3,190만 원이 발생합니다.

 

따라서 총 상환 금액은 1억 원의 원금과 약 3,190만 원의 이자를 합한 약 1억 3,190만 원입니다.

 

위의 과정을 표로 나타내면 아래와 같습니다. 

No	년도	원리금 상환액(만원)	상환 원금(만원)	잔금(만원)	연이자(만원)
1	1	2,638	1,638	8,362	1,000
2	2	2,638	1,802	6,560	836
3	3	2,638	1,982	4,578	656
4	4	2,638	2,180	2,398	458
5	5	2,638	2,398	0	240

 

결론: 채무자에게 어떤 방식이 더 이익인가

채무자에게 유리한 방식 1

 

결론부터 말씀드리면, 원리금 균등 상환 방식이 원금 균등 상환 방식보다 약 190만 원 더 많은 이자를 부담하게 됩니다.

(금액은 위의 실전 예시를 기준)

 

그 이유는 원리금 균등 상환 방식에서 이자가 남은 잔금에 붙기 때문입니다.

 

원금 균등 상환 방식은 초기에 원금을 많이 갚아나가기 때문에 잔금이 빨리 줄어들어 이자가 적게 발생합니다.

 

예를 들어, 첫 해와 두 번째 해에 각각 2천만 원씩 갚으면서 잔금이 크게 줄어듭니다.

 

반면, 원리금 균등 상환 방식에서는 초기 원금 상환액이 적어 첫 해에는 1,638만 원, 두 번째 해에는 1,802만 원밖에 상환하지 않아 잔금이 더 많이 남습니다.

 

예를 들어, 첫 해에는 원금 균등 상환 방식의 잔금이 8천만 원으로 줄어들지만, 원리금 균등 상환 방식은 8,362만 원, 즉 약 8,400만 원으로 더 많이 남습니다.

 

두 번째 해에도 원금 균등 상환 방식의 잔금은 6천만 원으로 줄지만, 원리금 균등 상환 방식은 약 6,600만 원으로 여전히 잔금이 더 많습니다.

 

이렇게 초기 원금 상환액의 차이 때문에 원리금 균등 상환 방식에서 더 많은 이자가 발생하게 됩니다.

 

대출자에게 유리한 방식은?

그렇다면, 대출자 입장에서 어느 방식이 더 유리할까요?

 

이자 부담 측면에서 보면 원금 균등 상환 방식이 유리합니다.

채무자에게 유리한 방식 2

 

하지만 원금 균등 상환 방식은 초기 상환액이 크기 때문에 초기에 재정적으로 부담이 될 수 있습니다.

 

반대로, 원리금 균등 상환 방식은 매년 상환 금액이 일정해 예측 가능성이 높고, 초기 부담이 상대적으로 적습니다.

 

그러나 그만큼 이자 부담이 커지게 됩니다. 따라서, 대출자의 재정 상황에 따라 적합한 방식이 달라질 수 있습니다.

 

초기 상환 부담을 줄이고 싶다면 원리금 균등 상환 방식을 선택하는 것이 좋을 수 있습니다.

 

반면, 전체 이자 부담을 줄이고자 한다면 원금 균등 상환 방식이 더 적합할 수 있습니다.

 

결론

결론적으로, 원금 균등 상환은 이자를 적게 내지만, 초기 상환 부담이 크고, 원리금 균등 상환은 초기 부담이 적지만 전체 이자가 더 많이 발생합니다.

 

따라서 이 두 상환 방식을 선택할 때는 본인의 재정 상황과 상환 계획을 충분히 고려해야 합니다.

 

대출은 신중하게 결정해야 하며, 불필요한 부채는 피하는 것이 좋습니다.

 

대출을 통해 부담을 줄이기보다는, 재정 상황을 미리 계획하고 관리하는 것이 중요합니다.

 

오늘은 원금 균등 상환과 원리금 균등 상환 방식에 대해 알아보았으니, 이 내용을 바탕으로 현명한 선택을 하시길 바랍니다.

 

대출 이자 계산기

마지막으로 대출 이자 계산기가 있는 곳을 안내해드립니다. 도움이 되기를 바랍니다.

대출 이자 계산기

 

본 포스팅은 지극히 개인의 주관적인 견해와 학습으로 작성된 것으로 어떠한 불법 복제 및 펌을 금지합니다.

 

또한 해당 포스팅을 활용한 어떠한 투자에도 책임이 없음을 알립니다.

부동산 양도세 절세 방법 과세표준과 세율

이주자택지 뜻, 이주자주택, 이주정착금, 토지보상

전세가율 높으면? 낮으면? 의미, 계산, 그래프